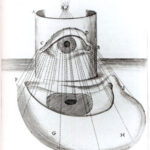
The Saphea Arzachelis Universal Astrolabe
The Universal Astrolabe is a different concept from the Planispheric Astrolabe… Some things
become easier on the Saphea, while some of the simplest things (like telling the time) become
trial and error. The main advantage of the Universal Astrolabe is that it is accurate at any given
latitude.
Stereographic Projection
The plates of both the Saphea Arzachelis and the Planispheric Astrolabe are drawn using the
same principle of stereographic projection, but the projections are cast from different points of
origin.
The Planispheric Astrolabe has the origin of its projection at the South Celestial Pole, and the
sky is then projected upwards onto the plane of the Equator.
With the Saphea Arzachelis, the origin of its projection is not at the bottom, but from both sides!
It has as its points of origin the Equinoxes (the points where the path of the Sun crosses the
Celestial Equator) and the sky is then projected onto the great circle of the Solstitial Colure.
With the exception of the signs of the Ecliptic, the Saphea’s plate is cast exactly the same
whether its point of origin is projected from the Vernal Equinox or the Autumnal Equinox!
The Position of the Sun on the Ecliptic.
On the plate of the Saphea, both of the Equinoxes are located at the point in the exact center of
the plate, where the vertical and horizontal diameters intersect.
Vertical diameter of the plate is called the Meridian, while the horizontal diameter of the
plate is called the Equinoctial line.
The plate of the Saphea Arzachelis
The Ecliptic is tilted at an angle of 23.4° and is labeled with the 12 zodiac signs.
Since the origin of the Saphea’s projection is from the side, the Ecliptic circle appears as a straight line on
its plate. To better understand the Saphea… let’s try to keep imagining the Ecliptic as a circle.
The Vernal Equinox appears at the very center of the plate, and from that point the path of the
Sun moves to the right (from Aries 0° through Gemini 30°) out to the circumference of the plate.
This point of the Ecliptic at the circumference represents the Summer Solstice with the
declination +23.4, and the Parallel that it intersects is the Tropic of Cancer.
The Sun then continues on its path, and moves to the left along the underside of the Ecliptic
line, (from Cancer 0° through Virgo 30°) until it arrives back at the centerpoint, which on the
underside is Libra 0°, the Autumnal Equinox.
Then continuing on the underside, the Sun moves left (from Libra 0° through Sagittarius 30°)
until it arrives at the circumference on the left side of the plate. This point of the Ecliptic
represents the Winter Solstice with the declination -23.4 on the plate, and the Parallel that it
intersects is the Tropic of Capricorn.
The Sun then travels to the right on the upper side of the Ecliptic line (from Capricorn 0° through
Pisces 30°) until it arrives back at the center point which is Aries 0°, the Vernal Equinox.
Just as a bit of trivia, the six Zodiac signs printed above the Ecliptic (Capricorn 0° to Gemini 30°)
have the origin of their stereographic projection at the Autumnal Equinox. To better understand
this, look at the back of your Planispheric Astrolabe and notice that these six signs fill the right
side of the calendar rings… and directly across from them on the left, with a perfect view, is the
Autumnal Equinox.
The Zodiac signs printed upside down below the Ecliptic (Cancer 0° to Sagittarius 30°) have the
origin of their stereographic projection at the Vernal Equinox. Again, notice that on the back of
the Planispheric Astrolabe, these six signs fill the left side of the calendar rings, and can be
perfectly viewed by the Vernal Equinox which is directly across from them on the right.
The Polar Arcs and Parallels.
Polar Arcs are the vertical ellipses on the plate and are drawn every 5°, which represent 20
minutes of time or Right Ascension. The bold Polar Arcs are drawn every 10°.
Three Polar Arcs equal 15° or one hour of time. The number to the left of every third Polar Arc
represents either the time of day or the hour angle of the Sun.
Parallels are the horizontal ellipses on the plate. Their primary function is to represent the
Declination of the Sun or the elevation above the local Horizon.
The border around the plate is divided into scales of four 90° quadrants. Upper right and
lower left quadrants are the same, so either of these scales can be used to measure the
Parallels by degrees. Upper left and lower right quadrants are also the same, and either can
be used to set the Regula to your current Latitude.
The Regula is the ruler that spins freely above the plate, and has a scale dividing it into 360
degrees. Connected to the Regula is a stiff jointed arm called the Brachiolus which is used to
pinpoint one particular location on the Saphea’s plate.
Time, Hour Angle and Right Ascension.
On the Planispheric Astrolabe, the 12 at the top represents Noon, and the 12 at the bottom
represents Midnight. When the Almuri on the Rete is set to 0°, (which is at the Meridian) the first
point of Aries (used to indicate Right Ascension) is pointed to 6 a.m. on the Limb.
When this is viewed from the side as we do with the Saphea, both 12 Noon and 12 Midnight are
located at the circumference of the plate. The upper line of numbers near the Tropic of Cancer
show the A.M. hours, and a lower line of numbers near the Tropic of Capricorn show the P.M.
hours.
Now remember on the Planispheric Astrolabe… that when the Almuri is set to 0°, the first point
of Aries indicates 6 A.M. on the Limb? Well, the Right Ascension on the Saphea also begins at
the ellipsis for 6 A.M…. which happens to be the vertical diameter of the plate!
Just as we imagined the line of the Ecliptic as a circle viewed from the side, try to imagine the
plate of the Saphea as a globe.
The measuring of Right Ascension starts at the Meridian Line (0 hrs 0 min) on the upper set of
numbers, then increases to the right until it reaches 6 hours of Right Ascension at the
circumference.
It continues around the back of this ‘globe’ on the lower set of P.M. hours from right to left, from
6 hours of Right Ascension at one circumference to 18 hours of Right Ascension at the other.
Then around to the front again on the upper A.M. numbers with 18 hours at the left
circumference and increasing to 24 hours of Right Ascension as we arrive back at the Meridian.
The plate isn’t labeled for Right Ascension and might be confusing (because it is marked only
for the time of day and hour angle) so when reading the upper numbers to the right, subtract 6
to find the Right Ascension. When reading the lower numbers heading left, add 6. Then back to
the upper numbers heading right, continue counting upwards towards 24.
The Saphea can be used to show three different coordinate systems.
- The Horizontal Coordinate system (which shows Altitude and Azimuth)
- The Equatorial Coordinate systems (which shows Right Ascension and Declination)
- The Ecliptic Coordinate system. (which shows Celestial Longitude and Celestial
Latitude)
Horizontal Coordinates
Poles represent the Zenith and Nadir of a specific latitude.
The Equinoctial line then represents the local Horizon.
Parallels represent Altitude and the Polar Arcs represent
Azimuth. (the angular distance of an object from 0° North)
Equinoctial line represents the Equator, the Polar Arcs represent Right Ascension and the Parallels represent Declination.
The Parallels above the Equinoctial line are positive declinations, while those below the Equinoctial line are negative declinations.
Ecliptic Coordinates
Rotate the plate so that the Ecliptic line is horizontal, and the Parallels above the Ecliptic line
now represent Celestial Latitude, and the Polar Arcs represent Celestial Longitude. The
Equinoctial line is then viewed as the Ecliptic, and the poles are viewed as the Ecliptic poles.
Now that we are familiar with the Saphea, let’s start the instructions!
Here are the principal applications of the Saphea Arzachelis Universal Astrolabe from the “De
Astrolabo Catholico” published in Latin at Antwerp, Belgium in 1556….
In our examples that follow, the day will be June 3rd, which is Gemini 13 on the Ecliptic. The
Declination of the Sun will be 22° 19’, (22.3°) and we’ll use my Latitude in Roundup, Montana at
46.3°
01: Find the position of the Sun on the Ecliptic for June 3rd.
The Sun’s position on the Ecliptic (also called its solar longitude) is found by using the calendar
rings.
- Place the edge of the Alidade to June 3rd on the calendar ring.
- Read the position of the Sun on the Ecliptic from the Zodiac ring.
On June 3rd, the position of the Sun is Gemini 13 on the Ecliptic.
02: Find the Declination of the Sun for Gemini 13.
If the line of the Ecliptic on your Saphea Arzachelis is marked in degrees, find the Parallel on
the plate that intersects with Gemini 13, and you’ll find 22.3° as the Declination of the Sun.
If only the Regula is marked in degrees, then rotate it to the line of the Ecliptic, and use its
degree scale to find the Parallel that intersects with Gemini 13.
- Find the beginning of Gemini on the plate.
- Now count 13 degrees on the Regula in the direction that the Sun is traveling on the
Ecliptic. - The point indicated on the line of the Ecliptic intersects with the Parallel on the plate for
Declination 22.3°
03: Find the Right Ascension of the Sun on June 3rd.
- Convert June 3rd to Gemini 13 on the calendar rings.
- Find Gemini 13 on the line of the Ecliptic and locate its nearest Polar Arc to the left.
If the location of the Sun is above the Ecliptic line, (as it is with Gemini 13) follow the Polar
Arc upwards to the time scale above. The hours are labeled to the left of the line they
represent. - From Gemini 13, the nearest Polar Arc to the left represents 10:40 of time. Subtract 6
and we have 4:40 hours of Right Ascension. - 1° = 4 minutes of time. The remaining 3° from the nearest Polar Arc to Gemini 13 equal
12 minutes. 3° x 4 minutes per degree = 12 minutes.
4:40 + 12 minutes= 4:52
The Right Ascension of the Sun on June 3rd is 4hrs 52min.
Instead of Gemini 13, what if the sign had been Cancer 13? Since this location of the Sun is
written below the Ecliptic line, (upside down) then follow the Polar Arc downwards to the time
scale below.
From Cancer 13, the nearest Polar Arc to the right represents 00:40 of time. Add 6 and we
have 6:40 hours of Right Ascension.
The remaining 3° from the nearest Polar Arc to Cancer 13 equals 12 minutes. 3° x 4 minutes
per degree = 12 minutes.
6:40 + 12 minutes = 6:52
For Cancer 13, the Right Ascension of the Sun is 6hrs 52min.
This is the way that Right Ascension was taught in the Latin manuscript written in 1556, but I
found another way that only uses the degree scale on the Regula. You may want to try this…
The signs that are written on the top of the Ecliptic line have their scale of degrees written on
the top line of the Regula, while the signs written underneath the Ecliptic line (upside down)
have their scale of degrees written underneath, on the second line of the Regula.
- Rotate the Regula to the Ecliptic. Gemini 13 is located 73° from the Meridian on the
upper line of the Regula’s degree scale.
Every 1° that the Sun travels = 4 minutes of time, and the Sun has traveled 73° from the
Meridian. - 73° x 4 min = 292 minutes.
- Divide 292 minutes by 60 minutes per hour. 292 ÷ 60 = 4.8666 hours.
- Convert .8666 from digital time back into minutes. .8666 x 60 = 52 minutes
The Right Ascension of the Sun when located at Gemini 13 is 4hrs 52min. - Again, instead of Gemini 13, what if the sign had been Cancer 13?. Since Cancer is on the
bottom side of the Ecliptic line, we read the degree scale on the bottom line of the Regula.
The scale on the Regula shows Cancer 13 to be 103° from the Meridian.
103° x 4 = 412 minutes
412 ÷ 60 = 6.8666
.8666 x 60 = 52 minutes
The Right Ascension of the Sun when its location is Cancer 13 = 6hrs 52min
This may be the long way around, and you may have a better way, but I find it to be easier than
following Polar Arcs.
04: Find the Maximum Noontime Altitude of the Sun.
Two pieces of information are required to find the Max Altitude of the Sun. These are the
Declination of the Sun and the Altitude of the Celestial Equator.
- Determine the declination of the Sun on June 3rd (Gemini 13) to be 22.3°
- Rotate the Regula to the Equinoctial Line and hold it steady, then position the Brachiolus
to 22.3° on the border of upper right scale of the Limb.
The altitude of the Celestial Equator is found by subtracting your Latitude from 90°. At my
Latitude of 46.3°, the altitude of the Celestial Equator is 43.7° (90° – 46.3° = 43.7°) - Rotate the Regula to place its edge at 43.7° in the upper right scale.
The Brachiolus indicates that the Maximum Noontime Altitude of the Sun on June 3rd is 66°
Altitude of the Equator + Declination = Maximum Noontime Altitude of the Sun
05: How to determine your current Latitude.
To find your current Latitude with the Saphea, three pieces of information are required. The
location of the Sun on the Ecliptic, (the solar longitude) the Declination of the Sun and its
Maximum Noontime Altitude.
- Use the calendar rings to convert June 3rd to Gemini 13 on the Ecliptic.
- On the plate, find Gemini 13 on the line of the Ecliptic. The Parallel that intersects with
Gemini 13 shows the Sun’s Declination to be 22.3°. - The next next step is to wait until the Sun crosses over the Meridian, at exactly Solar
Noon, and use the Alidade to take the Altitude of the Sun. At latitude 46.3, the Max
Altitude of the Sun is 66° on June 3rd.
(Here’s another method that you can use anytime. Rotate the Rete on the back to place Gemini
13 directly over the Meridian. The Maximum Noontime Altitude of the Sun is shown by the
Almucantars to be 66°)
Now we can use the Declination of the Sun and its Maximum Noontime Altitude to determine
our Latitude. - Rotate the Regula to the Equinoctial line at 0°, and hold it there firmly.
- Adjust the tip of the Brachiolus so it points to the Sun’s Maximum Noontime Altitude of
66° in the upper right scale of the limb. - Without changing the arrangement, rotate the Regula and Brachiolus clockwise (using
the same upper right scale) until the tip of the Brachiolus points to 22.3° (the Declination
of the Sun on June 3rd)
In this position, the Regula represents the local horizon and the scale in the lower right quadrant
shows the current latitude! Counting from 0° at the South Celestial Pole, the scale shows 46.3°
latitude. 😃
90° – Equator = Latitude
90° + Declination – MaxH = Latitude
06: Find the Sun’s Altitude by knowing its Declination.
With the Regula set to your Latitude and the Brachiolus set to the Declination of the Sun, you
can find the Altitude of the Sun for any hour of the day.
- Set the Regula to your Latitude on the degree scale in the lower right quadrant. (46.3)
- Adjust the Brachiolus to the position where the 9 a.m. / 3 p.m. Polar Arc crosses the
Declination Parallel for 22.3o (Gemini 13) - Rotate both the Regula and Brachiolus from your latitude to the Equinoctial Line. The tip
of the Brachiolus is now pointing to the Parallel for the Sun’s Altitude of 46°
At both 9 a.m. and 3 p.m. the Altitude of the Sun will be 46°. Try it with any Polar Arc to see the
Sun’s Altitude at that hour.
07: How to calculate the Declination of a star.
The Meridian is the line in the sky that begins due North of you, passes through the North
Celestial Pole and the Zenith directly over your head, then down to the horizon due South of
you.
To calculate the Declination of a star, you need to measure its Maximum Altitude as it crosses
the Meridian, then subtract the Altitude of the Celestial Equator.
The equation to determine the Altitude of the Celestial Equator above the horizon is:
90°- Latitude = Equator
So…
90° – 46.3° = 43.7°
43.7° is the Altitude of the Celestial Equator at my Latitude.
The equation to find Declination is:
Max Altitude – Altitude of Equator = Declination
Stars that are North of the Celestial Equator have a positive (+) declination, and stars that are
South of the Celestial Equator have a negative (-) declination.
If Arcturus is observed crossing the Meridian at its Maximum Altitude of 62.7°, then:
62.7° Max Altitude – 43.7 Equator = 19° Declination of Arcturus.
The Declination of Arcturus is +19°
If Spica is observed crossing the Meridian at its Maximum Altitude of 32.4°, then:
32.4° Max Altitude – 43.7 Equator = -11.3 Declination of Spica.
The Declination of Spica is -11.3
08: Find the location of the Sun on the Ecliptic without knowing
today’s date.
- Set the Regula to your current Latitude by using the lower right scale. (46.3°)
- Find the current Declination of the Sun by subtracting the Altitude of the Equator (43.7°)
from the Sun’s Maximum Noontime Altitude. (66°)
66° – 43.7° = 22.3°
(Since this exercise is done without knowing today’s date, we’ll have to get the Maximum
Altitude of the Sun by observation at Solar Noon) - Find the point where the 22.3° declination parallel intersects the ecliptic line to find the
Solar Longitude to be Gemini 13.
Use the calendar rings to find today’s date to be June 3rd.
09: Find the Right Ascension and Declination of a star given its
Ecliptic longitude and latitude.
Consider the Equinoctial line to represent the projection of the Ecliptic. The coordinates then
become Ecliptic coordinates so the Polar Arcs indicate celestial longitude and the Parallels
indicate celestial latitude.
- Place the Regula over the Equinoctial line. Put the tip of the Brachiolus on the point
having the given Ecliptic longitude and latitude. (the intersection of the Polar Arc and
Parallel) - Now rotate the entire Regula assembly to the Ecliptic line.
The coordinates are now Equatorial. The Brachiolus points to the Polar Arc for Right Ascension
and to the Parallel for Declination.
Also, by rotating the Arzachelis Plate by an angle equal to your latitude, the Equator becomes
the horizon. The North Celestial Pole now becomes the Zenith, meaning the line connecting the
Pole to the Equator becomes the line connecting the Zenith to the local horizon. The Parallels
then become lines of Altitude.
10: Find the time of Sunrise and Sunset, as well as the path of the Sun
across the sky for June 3rd.
- Set the Regula to your current Latitude (46.3) by using the scale on the lower right
quadrant. The Regula now represents the local Horizon. - Use the calendar rings to convert June 3rd to Gemini 13.
- Locate Gemini 13 on the Ecliptic line and find the Parallel on the plate that intersects it.
- Follow that Parallel to where it meets the Regula, and the Polar Arc on the plate gives
you the time of Sunrise. Each of the Polar Arcs represent 20 minutes, so the time of
Sunrise is 4:20 a.m. Local Solar Time. - Follow the same Polar Arc to the P.M. hours on the underside of the Regula to find the
time of Sunset as 7:40 p.m. Local Solar Time.
Notice that if you add the time of Sunrise to the time of Sunset, the result is 12. This means that
another way to find the time of Sunset (without using the plate) is to subtract the time of Sunrise
from 12.
12:00 – 4:20 = 7:40
The Gemini 13 Parallel that you just followed to the Regula represents the Sun’s Diurnal Arc
(path across the sky) for June 3rd. The Parallel shows the length of time between Sunrise (at
the Regula) and Noon, (at the circumference) then it returns along the Declination Parallel from
Noon (at the circumference) to Sunset. (at the Regula)
Solar Noon is the exact middle of the day. If the Sun has set 7 hours and 40 minutes after Noon,
then the Sun rose 7 hours and 40 minutes before Noon. You can determine the length of day by
multiplying the time of Sunset x 2.
7:40 x 2 = 15:20
The length of the day on June 3rd is 15 hours and 20 minutes.
In the same way, Midnight is the exact middle of the night. If the Sun rose 4 hours and 20
minutes after Midnight, then the Sun set 4 hours and 20 minutes before Midnight. You can tell
the length of the night by multiplying the time of Sunrise x 2.
4:20 x 2 = 8:40
The length of the night on June 3rd is 8 hours and 40 minutes.
Notice that if you add the length of day to the length of night, the result is 24.
12: Find your Local Solar Time by the Altitude and Declination of the
Sun.
- Measure the Sun’s Altitude with the Alidade, and find it to be 35°.
- Set the Regula to your local Latitude. In my case, 46.3
- Put the tip of the Brachiolus on any point of the Declination Parallel corresponding to
Gemini 13 (22.3°) - Note the time shown by the Brachiolus on the Polar Arcs, then rotate the Regula to the
Equinoctial Line. - Now determine the Parallel that the tip of the Brachiolus falls on in the second position. If
this Parallel is exactly that of the observed altitude of the Sun, then the position of the
Brachiolus was correct and the time noted was exact.
If the tip of the Brachiolus does not fall on the desired Parallel, then you must start over and
continue with successive approximations.
On June 3rd, when the Sun is 35° above the horizon, the Local Solar Time is 7:55 a.m. or 4:05
p.m.
13: Find the Hour Angle of a star by its Altitude and Declination
- Take the altitude of the star with the alidade.
- Put the tip of the Brachiolus at any point on the Parallel corresponding to the star’s
Declination. - Note the hour angle shown by the Brachiolus on the Polar Arcs, then rotate the Regula
to the Equinoctial line. - Now Determine the Parallel that the tip of the Brachiolus falls on in the second position.
If this Parallel is exactly that of the observed altitude, then the position of the Brachiolus
was correct and the time noted is the hour angle of the star.
If the tip of the Brachiolus does not fall on the desired Parallel, then you must start over and
continue with successive approximations.
14: To find the time using the Hour Angle of a star
Following the same steps that we used to find the Local Solar Time, we found the Hour Angle of
a star by its Altitude and Declination.
Now we can find the Local Solar Time by using these three things: The Hour Angle of the star,
the Right Ascension of the star, and the Right Ascension of the Sun.
For our example, the Brachiolus just pinpointed the Hour Angle of Vega over the 9 p.m. ellipsis
on the plate.
The Right Ascension of Vega = 18h 36m.
The Right Ascension of the Sun’s = 17h 16m.
- Subtract the Sun’s R.A. (17h 16m) from Vega’s R.A. (18h 16m).
18h 36m – 17h 16m = 1h 20m. This is Vega’s delay in relation to the Sun. - Adding Vega’s delay in relation to the Sun (1h 20m) to Vega’s hour angle (9h) gives us a
final figure of 10:20 p.m. Local Solar Time.
15: If your Saphea is equipped with a Rete:
This operation may be solved graphically on the astrolabe as follows:
a. If the astrolabe is complete with a rete (Astrolabum Catholicum of Gemma Frisius), the rete is
oriented by placing the rule on the index of the star so the rule shows the hour angle found
above.
Without touching the rete, direct the rule to the angle of the ecliptic where the Sun is found on
the day under consideration and the rule will then show the required time on the limb.
b. Certain Saphaeae do not include a rete but the zodiacal calendar is engraved on an
independent disk on the back, which is moveable about the center of the instrument. (Saphaea
cum Zodiaco mobile) This disk bears engraved reference points corresponding to the right
ascension of the principal stars. The method of operation is as follows:
Turn the plate in question so the reference point corresponding to the observed star is opposite
the angle on the limb corresponding to the hour angle.
In this position the zodiacal degree of the day under consideration is opposite the degree on the
limb marking the required time.